ELETRO-RÁDIO-TÉRMICA QUÂNTICA RELATIVISTA GRACELI

ELETRO -RÁDIO - TERMO QUÂNTICA RELATIVISTA GRACELI.

N=N_{o}.e^{-\lambda .t}

/ ${\mathcal {T}}$

Para calcular a probabilidade de um processo de espalhamento relativístico, é necessário determinar a chamada amplitude de espalhamento invariante de Lorentz, ${\mathcal {M}}$ , que conecta um estado inicial, $\psi _{i}$ , caracterizado por um conjunto de partículas que possuem momentos bem definidos, a um estado final, $\psi _{f}$ , contendo outras partículas (na maioria das vezes diferentes) que também possuem momentos bem definidos.^[31]

Para fazer uso da técnica gráfica criada por Feynman é importante saber que cada diagrama de Feynman representa uma contribuição para ${\mathcal {M}}$ . Isto significa que cada diagrama representa uma função complexa escrita em termos dos momentos externos. Ou seja, os diagramas fornecem um maneira pictórica de representar as contribuições para a amplitude ${\mathcal {M}}$ . Uma vez determinada uma amplitude é possível calcular grandezas física mensuráveis como a seção de choque diferencial,^[32]^[33] assim, o diferencial dessa seção efetiva será uma função do módulo quadrático da amplitude de espalhamento:

$\mathrm {d} \sigma ={\frac {1}{E^{2}}}\,|{\mathcal {M}}|^{2}\mathrm {d} \Omega$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

As regras de Feynman que traduzem diretamente um diagrama em uma contribuição de ${\mathcal {M}}$ , correspondem um fator algébrico a cada elemento e o produto desses fatores dá o valor dessa contribuição (a soma das contribuições dá um valor aproximado de ${\mathcal {M}}$ .^[33]

Para a manipulação das fórmulas algébricas, é preciso utilizar o sistema de unidades naturais onde a constante de Planck reduzida ( $\hbar$ ) e a velocidade da luz ( $�$ ) são as unidades, ficando assim: $\hbar =c=1$ .

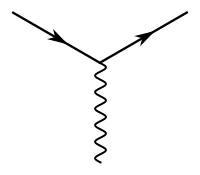
Dessa forma, as Regras de Feynman para o cálculo $-i{\mathcal {M}}$ na eletrodinâmica quântica será:

Categoria	Spin	Partículas	Fator Multiplicador
Linhas Externas	0	Bóson de Entrada	1
	0	Bóson de Saída	1
	0	Anti-Bóson de Entrada	1
	0	Anti-Bóson de Saída	1
	½	Férmion de Entrada	$�$
	½	Férmion de Sáida	${\bar {u}}$
	½	Anti-Férmion de Entrada	${\bar {v}}$
	½	Anti-Férmion de Saída	$�$
	1	Fóton de Entrada	$\epsilon _{\mu }$
	1	Fóton de Saída	$\epsilon _{\mu }^{*}$
Propagadores (Linhas Internas)	0	Bóson	${\frac {i}{q^{2}-m^{2}}}$
	½	Férmion	${\frac {i(q\!\!\!/+m)}{q^{2}-m^{2}}}$
	1	Partícula sem Massa (Fóton)	${\frac {-ig_{\mu \nu }}{q^{2}}}$
	1	Partícula com Massa (Bóson)	${\frac {-i(g_{\mu \nu }-q_{\mu }q_{\nu }/m^{2})}{q^{2}-m^{2}}}$
Vértice			$-ig_{e}\gamma ^{\mu }$

Onde:

$�$ e $�$ são os espinores de Dirac, com $u(p)$ normalizado: ${\bar {u}}(p)u(p)=2m$ ;
$\epsilon _{\mu }$ é o vetor de polarização circular do fóton;
$�$ é a massa da partícula;
$�$ é a unidade imaginária;
$q\!\!\!/=\gamma ^{\mu }q_{\mu }$ são os quatro momentos $q_{\mu }$ e a matriz de Dirac $\gamma ^{\mu }$ ;
$g_{\mu \nu }$ é a métrica de Minkowski;
$g_{e}$ é a carga do elétron.

Matematicamente, a eletrodinâmica quântica tem a estrutura da teoria de calibre do grupo abeliano e possui um grupo de simetria de calibre U(1). O campo de medida da interação entre o campo carregado de spin -1/2 é o campo eletromagnético. Assim, usando o sistema de unidade natural como sendo $c=\hbar =\mu _{0}=1$ , o lagrangiano na EDQ que provome^{[necessário esclarecer]} a mediação na interação entre vários elétrons ou pósitrons por meio de fótons é dada por:^[32]^[33]

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

Onde:

$\gamma ^{\mu }$ são as matrizes de Dirac;
$\psi$ é o campo espinor duplo das partículas de spin 1/2 (como o campo elétron-pósitron);
${\bar {\psi }}\equiv \psi ^{\dagger }\gamma ^{0}$ é o adjunto de Dirac;
$D_{\mu }$ é a derivada covariante de calibre;
$�$ é a unidade imaginária;
$�$ é a massa do elétron;
$F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }$ é o tensor do campo eletromagnético.

Equação da ação

O lagrangiano EDQ para um campo de spin-1/2 interagindo com o campo eletromagnético em unidades naturais dá origem à ação:^[32]

Ação na EDQ

$S_{\text{QED}}=\int d^{4}x\,\left[-{\frac {1}{4}}F^{\mu \nu }F_{\mu \nu }+{\bar {\psi }}\,(i\gamma ^{\mu }D_{\mu }-m)\,\psi \right]$

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

Onde:

$D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }$ $D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }$ é a derivada covariante de calibre;
- $�$ é a constante de acoplamento , igual à carga elétrica do campo bispinor;
- $A_{\mu }$ é o quatro potencial covariante do campo eletromagnético gerado pelo próprio elétron. Também é conhecido como campo de calibre ou $U(1)$ conexão;
- $B_{\mu }$ é o campo externo imposto pela fonte externa.

A expansão da derivada covariante revela uma segunda forma útil do lagrangiano (campo externo $B_{\mu }$ definido como zero para simplificar):

${\mathcal {L}}=-{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }+{\bar {\psi }}(i\gamma ^{\mu }\partial _{\mu }-m)\psi -ej^{\mu }A_{\mu }$

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

Sendo $j^{\mu }$ o conservado $U(1)$ corrente decorrente do teorema de Noether: $j^{\mu }={\bar {\psi }}\gamma ^{\mu }\psi .$

Expandindo a derivada covariante no lagrangiano é obtida a seguinte expressão:

${\mathcal {L}}=-{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }+i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma ^{\mu }A_{\mu }\psi -m{\bar {\psi }}\psi$ $=-{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }+i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -m{\bar {\psi }}\psi -ej^{\mu }A_{\mu }.$

$N=N_{o}.e^{-\lambda .t}$

E pela simplificação, $B_{\mu }$ foi definido como zero. De maneira alternativa, é possível absorver $B_{\mu }$ em um novo campo de medição $A'_{\mu }=A_{\mu }+B_{\mu }$ e renomear o novo campo como $A_{\mu }$ . Dessa forma, a partir deste lagrangiano, as equações de movimento para o campos $\psi$ e $A_{\mu }$ podem ser obtidas.

Equação de movimento para Ψ

Essa equação surge de forma mais direta considerando a equação de Euler-Lagrange para ${\bar {\psi }}$ , pois como o lagrangiano não contém $\partial _{\mu }{\bar {\psi }}$ termos, obtemos imediatamente:

${\frac {\partial {\mathcal {L}}}{\partial {\bar {\psi }}}}=0$

Permitindo, assim, que a equação do movimento para $\psi$ possa ser escrita desta forma:

$(i\gamma ^{\mu }\partial _{\mu }-m)\psi =e\gamma ^{\mu }A_{\mu }\psi .$

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

Equação de movimento para Aμ

No equacionamento dessa equação é preciso usar a equação de Euler-Lagrange para o campo $A_{\mu }$ :

$\partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)-{\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=0,$

Com as derivadas sendo:

$\partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)=\partial _{\nu }\left(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }\right)$

${\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=-e{\bar {\psi }}\gamma ^{\mu }\psi .$

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

E substituindo esses dois termos de volta na equação de Euler-Lagrange trabalhada anteriormente é possível obter:

$\partial _{\mu }F^{\mu \nu }=e{\bar {\psi }}\gamma ^{\nu }\psi$

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

Que também pode ser escrito em termos de $j^{\mu }$ da seguinte forma:

$\partial _{\mu }F^{\mu \nu }=ej^{\nu }.$

$/$ $N=N_{o}.e^{-\lambda .t}$ / ${\mathcal {T}}$

Agora, se a condição de calibre de Lorenz é adotada, pode-se obter:

$\partial _{\mu }A^{\mu }=0,$

$N=N_{o}.e^{-\lambda .t}$

E as equações se reduzem a:

$\Box A^{\mu }=ej^{\mu }$

$N=N_{o}.e^{-\lambda .t}$

Onde:

$\Box$ representa o Operador de d'Alembert.

Assim, é possível alcançar uma equação de onda para o quatro potencial, sendo a versão da eletrodinâmica quântica das equações clássicas de Maxwell no medidor de Lorenz.

Search This Blog